TLS Notary
| Abstract | TLSNotary is a browser add-on which allows you (the auditee) to prove to the auditor that a certain HTTPS page is present in a web browser, without compromising your internet connection, passwords or credentials. TLSNotary can be used e.g. to prove to the auditor that you made an online bank transfer. TLSNotary does not do man-in-the-middle snooping, but relies on SSL/TLS cryptography. TLSNotary page captures are non-forgeable. |
|---|---|
| Year | |
| Link to the paper | https://tlsnotary.github.io/docs-mdbook/ |
| Relevance score | Very relevant |
| Quality score | 5 |
| Labels | Legacy compatiblePossible tool in larger solutionWeb2 to Web3 data transfer |
TL;DR
Assuring the authenticity of the data that is pulled from web2 servers is an important task for the next phases of the Lido project. For the first phase, we check the existing solutions such as DECO, TLSNotary, and TLS-N. We examined the DECO and TLS-N protocol in separate notes.
TLSNotary is a protocol that allows a user (Requester) to prove to a verifier (Notary) that he interacted with a certain Server and that the transcript between them was not altered. It is a modified version of the standard TLS protocol.
The main idea of the TLSNotary protocol is to split the session keys of the client into two parts, and the Requester and the Notary participate in a two-party computation (2PC) with their key shares to jointly communicate with the server. Neither the Requester nor the Notary knows the session keys. They only have shares of them.
The first version of TLSNotary released in 2014 [1] only supports TLS 1.1 and older versions. However, we see that the TLSNotary protocol is updated so that it supports TLS 1.2 and newer versions.
Preliminary
There are three parties in the TLSNotary protocol, i.e. Requester, Notary, and Server.
The Requester
It is the party that interacts with the Server through a TLS session. The Requester can encrypt a request with a session key, and send it to the Server. Upon receiving the encrypted response from the Server, the Requester gets help from the Notary to decrypt it. Only the Requester can see the decrypted data.
The Notary
It is the party that the Requester aims to convince. He holds partial session keys, and he participates in two-party computation (2PC) with the Requester to achieve the TLS session. He doesn’t see the decrypted response of the Server, but he has a commitment to the decrypted data.
The Server
It is a standard party in a TLS session. It can be any server supporting TLS protocol. The protocol is transparent to the Server, i.e. the Server cannot distinguish whether it interacts with a client for a standard TLS or a TLSNotary session.
TLSNotary
First, we see the general workflow in the below figure, then we’ll describe each building block in the next sections.
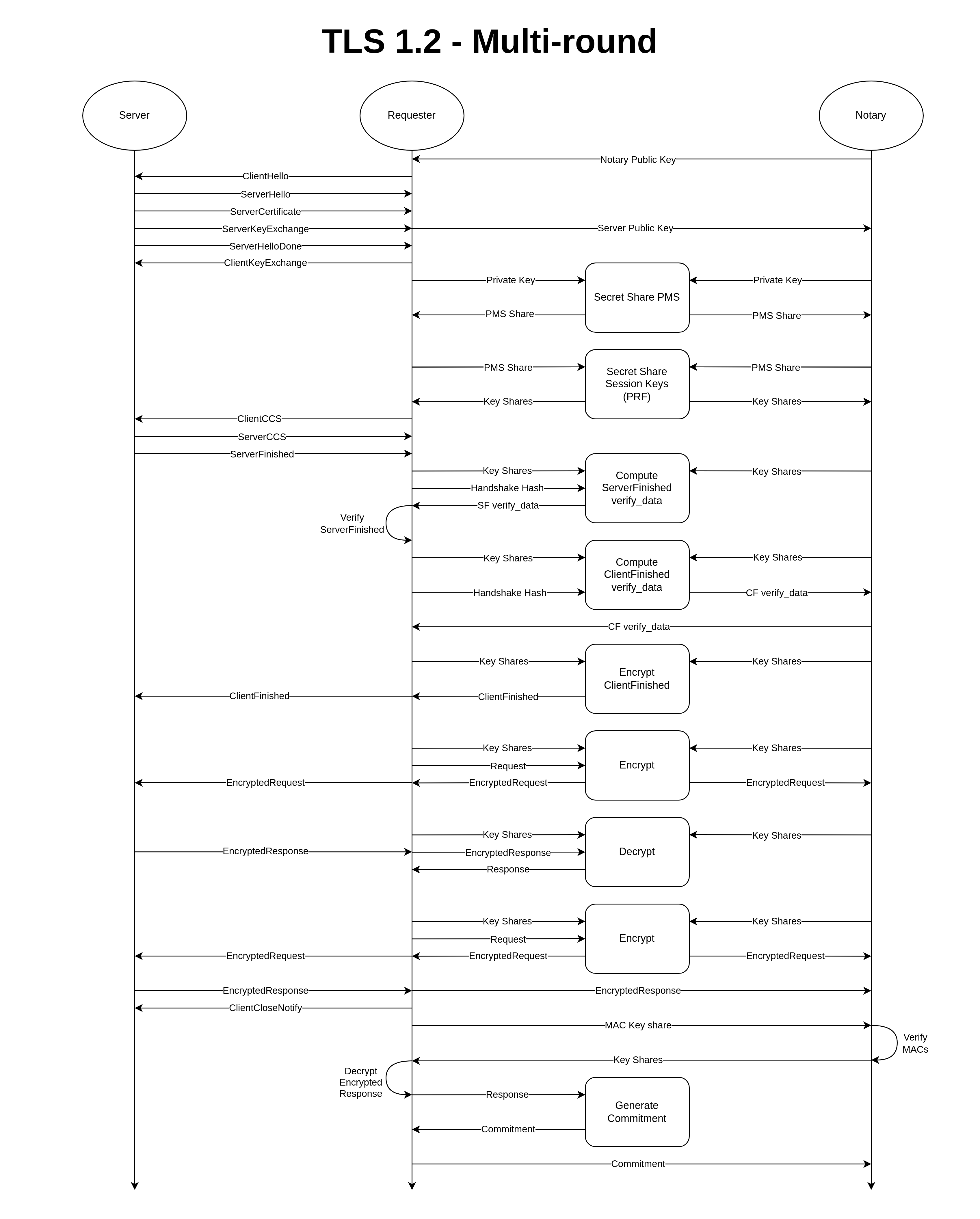
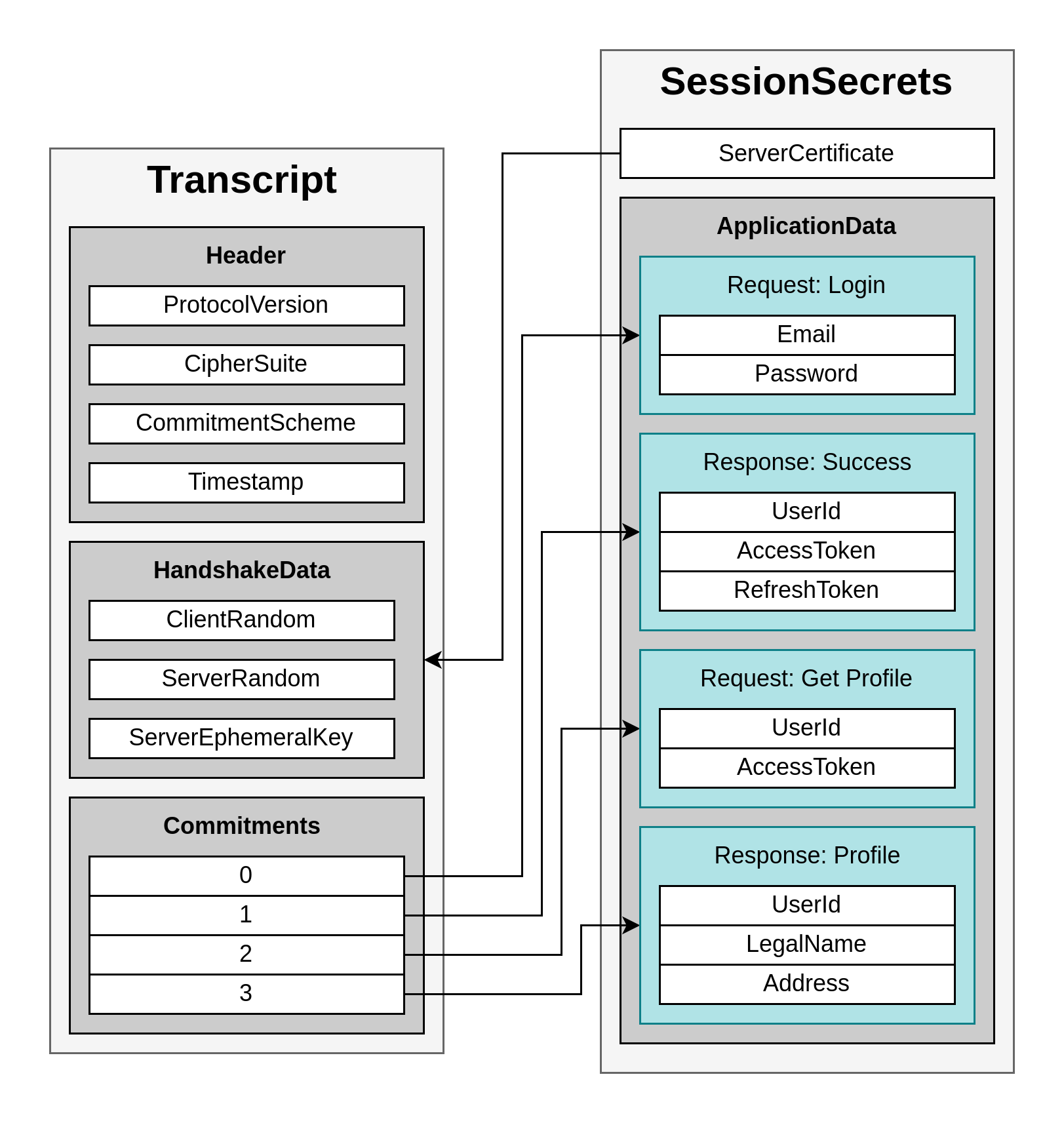
Transcript
The Transcript is a collection of data that includes metadata, handshake data, and the commitments to the requests and the responses. If the Notary is not the verifier, the Notary is required to sign the Transcript to present it to a verifier.
Key Exchange
In all versions of the TLS protocol, the session keys are obtained by a key exchange protocol. To that end, the Server, the Requester, and the Notary participate in the below Elliptic Curve Diffie-Hellman (ECDH) key exchange protocol. Assume that is an elliptic curve group with prime order and generator .
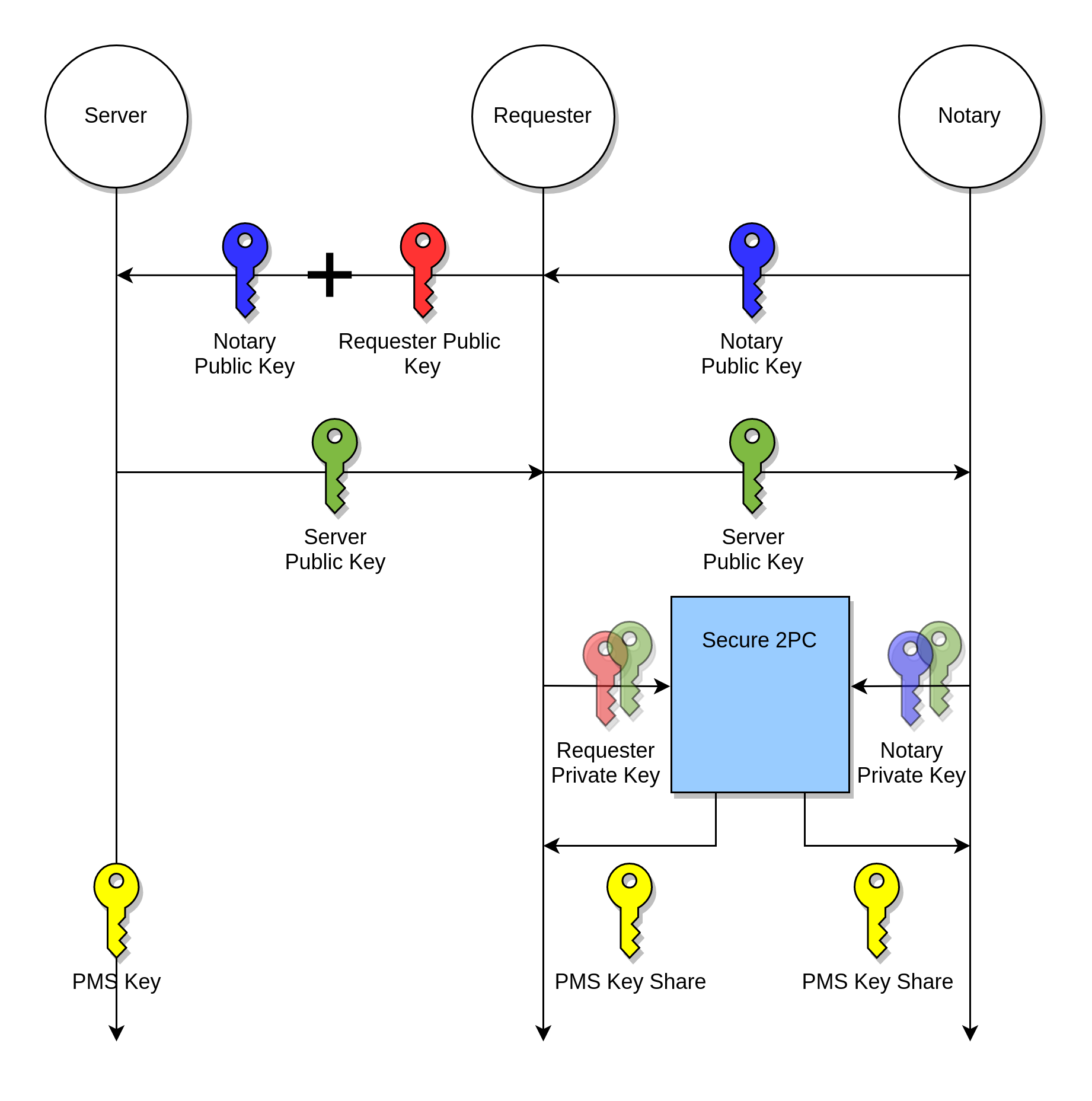
The 3-party ECDH protocol between the Server, the Requester, and the Notary results in Pre-master Secret (PMS) shares for the Requester and the Notary as follows:
- The Server sends its public key to the Requester, and the Requester sends it to the Notary.
- The Requester picks a random private key , and computes his public key
- The Notary also picks a random private key , and computes his public key
- The Notary sends his public key to the Requester.
- The Requester computes the client public key , and sends it to the Server.
- The Requester computes the elliptic curve point
- The Notary computes the elliptic curve point
- Addition of the elliptic curve points and results in , where is the PMS (note that is not used in TLS)
Now the goal is to compute by a secure two-party computation.
To do that, an M2A (multiplicative-to-additive) and A2M (additive-to-multiplicative) protocols from [7] are used.
- Apply A2M to and obtain .
- Apply A2M to and obtain .
- Now we can rewrite as
- ,
- can be computed by the Notary, he obtains ,
- can be computed by the Requester, he obtains .
- Now we have .
- Now apply M2A to to obtain .
- We have
- The PMS share of the Notary is
- The PMS share of the Requester is
Key derivation
The Requester and the Notary must run the PRF -a secure 2PC- with their PMS shares as inputs
- to compute the symmetric keys that will be used in communication with the Server, and
- to compute the
verify_datafor theClient_Finished and theServer_Finished messages.
The PRF function is computed via an as follows:
- The Requester and the Notary participate in a 2PC to compute a PRF (see the above equation) that outputs the master secret .
- Using as the input, they compute their expanded key shares by 2PC.
- Upon having expanded key shares, the Requester and the Notary jointly compute the message and the
verify_datathat depends on random seeds, , and the hash of the handshake data up to this point. (see the below code)# (handshake_hash) is a sha256 hash of all TLS handshake messages up to this point seed = str.encode('client finished') + handshake_hash a0 = seed a1 = hmac.new(ms, a0, hashlib.sha256).digest() p1 = hmac.new(ms, a1+seed, hashlib.sha256).digest() verify_data = p1[:12]
- Then the Requester proceeds to encrypt and authenticate the
verify_dataand sends it to the Server.
- Once the Requester receives the from the Server, the Requester and the Notary jointly compute the
verify_datafor .
- They proceed to decrypt and authenticate the data in 2PC. Then the Requester checks whether the
verify_datathat they compute matches the decrypted one.
We skip the details on 2PC. For further information please see here.
Commitment
At the end of the TLSNotary protocol, the Requester has some encrypted data (AES ciphertext). Although this may also be seen as a commitment to a plaintext, this kind of commitment is not flexible enough, especially for cases when a Requester wants to partially reveal the plaintext.
So, how can a Requester transform the ciphertext into a commitment?
It is stated in the documents that proving the decryption in zero-knowledge is not the computationally cheapest way to do that. For the same purpose, two approaches are proposed:
- Decrypting the ciphertext with Garbled Circuits and producing a hash commitment to the wire labels. (useful for committing to the data to be made public)
- Producing a Poseidon hash over the private data (useful for proving the statements about some private data in zero-knowledge)
We skip the details. For further information please see here.
Implementation
- In 2015, the first version of PageSigner, which is a Chrome extension for the TLSNotary client side, was announced.
- In 2020, PageSigner v.2 (supporting TLS 1.2) was announced.
- On November 21, 2021, Pagesigner v.3 was announced. (supporting TLS 1.2+)
Comparison of DECO and TLSNotary
Both protocols seem to be WIP, they haven’t been released yet. We compare them according to the DECO paper and TLSNotary sources in the references. Note that the TLSNotary documentation and GitHub repositories are not very clear to compare it to the DECO paper.
TLSNotary and DECO protocols have the same functionalities, and they use the same building blocks such as garbled-circuits protocols [13], A2M (Additive-to-multiplicative), M2A (multiplicative-to-additive) share conversion protocols [7][14], etc., for achieving those functionalities.
We give some possible differences below:
- Both protocols support the AES cipher in two modes: CBC-HMAC and GCM.
- For the premaster secret share generation
- The DECO paper proposes to use the M2A protocol using Paillier homomorphic encryption in [14], and The TLSNotary documents propose to use A2M and M2A protocol implementations from [7].
- For the CBC-HMAC cipher suit, DECO paper proposes to split the MAC key into two parts, for the prover and the verifier, and the encryption key is directly given to the prover. However, the TLSNotary documents do not specify the encryption key and the MAC key clearly.
- For the AES GCM cipher suit, both protocols proceed similarly.
- DECO paper uses garbled circuit protocol from [13]. TLSNotary proposes to use the Dual Execution protocol [15] as 2PC HMAC computations.
- For encryption of the client’s query and the decryption of the server’s response
- For the CBC-HMAC cipher suit,
- DECO paper proposes to generate the tag with a 2PC of HMAC, but the encryption is done by only the prover.
- TLSNotary documents do not specify how it is done. According to the figure on the GitHub page, both encryption and decryption are performed by a 2PC.
- For the CBC-HMAC cipher suit,
- For committing the data and the proof generation,
- the DECO paper proposes to use a technique called selective opening that allows the prover to efficiently reveal or redact substrings in plaintext. The main idea is to prove in zero-knowledge that the last three blocks of ciphertext are the encrypted tag data.
- On the other hand, TLSNotary documents state that proving the decryption of the ciphertext in zero-knowledge is computationally expensive. Instead, it proposes
- to decrypt the ciphertext with garbled circuits and produce a hash commitment to the wire labels. (useful for committing to the data to be made public)
- to produce a Poseidon hash over the private data (useful for proving the statements about some private data in zero-knowledge)
- Security:
- DECO protocol UC-securely realizes in the -hybrid world, against a static malicious adversary with abort. See Theorem 4.1 in the DECO paper.
- We couldn't see any adversarial assumption or security analysis in the TLSNotary documents.
References
- Efficient Secure Two-Party Exponentiation https://www.cs.umd.edu/~fenghao/paper/modexp.pdf
- POSEIDON: A New Hash Function for Zero-Knowledge Proof Systems https://eprint.iacr.org/2019/458.pdf
- Hubert Ritzdorf, Karl Wüst, Arthur Gervais, Guillaume Felley, and Srdjan Čapkun. 2018. TLS-N: Non-repudiation over TLS Enabling Ubiquitous Content Signing.. In NDSS https://eprint.iacr.org/2017/578.pdf
- Xiao Wang, Samuel Ranellucci, and Jonathan Katz. 2017. Authenticated Garbling and Efficient Maliciously Secure Two-Party Computation. In ACM CCS. https://eprint.iacr.org/2017/030
- Rosario Gennaro and Steven Goldfeder. 2018. Fast multiparty threshold ECDSA with fast trustless setup. In ACM CCS. https://eprint.iacr.org/2019/114.pdf
- A Pragmatic Introduction to Secure Multi-Party Computation https://securecomputation.org/docs/pragmaticmpc.pdf
- Aug 2019. (Bristol Format) Circuits of Basic Functions Suitable For MPC. https://homes.esat.kuleuven.be/~nsmart/MPC/old-circuits.html.