DECO

Abstract	Thanks to the widespread deployment of TLS, users can access private data over channels with end-to-end confidentiality and integrity. What they cannot do, however, is prove to third parties the provenance of such data, i.e., that it genuinely came from a particular website. Existing approaches either introduce undesirable trust assumptions or require server-side modifications. As a result, the value of users' private data is locked up in its point of origin. Users cannot export their data with preserved integrity to other applications without help and permission from the current data holder. We propose DECO (short for decentralized oracle to address the above problems. DECO allows users to prove that a piece of data accessed via TLS came from a particular website and optionally prove statements about such data in zero-knowledge, keeping the data itself secret. DECO is the first such system that works without trusted hardware or server-side modifications. DECO can liberate data from centralized web-service silos, making it accessible to a rich spectrum of applications. To demonstrate the power of DECO, we implement three applications that are hard to achieve without it: a private financial instrument using smart contracts, converting legacy credentials to anonymous credentials, and verifiable claims against price discrimination.
Year	2019
Link to the paper	https://www.deco.works/
Relevance score	Very relevant
Quality score	5
Labels	ImplementationsLegacy compatibleManagement of credentialsPossible tool in larger solutionSybil resistance insights

TL;DR

DECO is a protocol that enables users to prove (potentially in zero-knowledge) to a verifier that he pulled a piece of data from a certain web server via a TLS channel. Unlike Town Crier or TLS-N, it works without trusted hardware or modification on the server side.

The main idea is to share the client keys among the prover and the verifier so that they can jointly act as a single client like in a standard TLS protocol. Note that a server cannot distinguish whether it interacts with a client of a TLS session or a tuple of prover and verifier in a DECO protocol.

Preliminary

Roles

Server( $\mathcal{S}$ ): Data source which supports the TLS protocol.

Prover( $\mathcal{P}$ ): Off-chain repeater that requests data from the server, generates a proof of validity, then sends it to the verifier.

Verifier( $\mathcal{V}$ ): On-chain Oracle node, receives the data and proof from the prover and verifies its correctness.

Notation

$sid$ : the session ID, unique per session.

$r$ : randomly generated bit string.

$Q$ : query information.

$R$ : response information.

$\mathcal{\sigma}$ : signature.

$τ$ : MAC tag.

Transport Layer Security (TLS) protocol

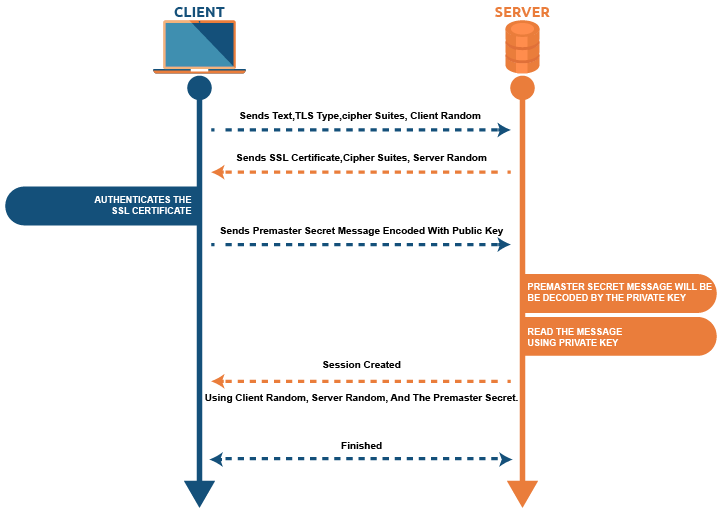
Source: https://www.ssl2buy.com/wiki/wp-content/uploads/2021/02/ssl-tls-handshake.png Figure 1. This figure depicts the general workflow of a TLS handshake.

The client sends “client hello” to the server, along with TLS type, and cipher suite with a random $r^c$ generated by the client.

The server receives the data, and sends “server hello” to the client, along with a certificate, cipher suite with a random $r^s$ generated by the server, and the server’s public key $K^s$ .

The client receives the data, and generates a random premaster secret $r^{ps}$ , encrypts it with $K^s$ , and sends it to the server.

The server using the secret key decrypts the message and obtains $r^{ps}$ . For both server and client, the session key is $r^c+r^s+r^{ps}$ .

The server uses the session key with symmetric encryption to encrypt the handshake completes the message and sends it to the client. TLS handshake complete.

DECO Protocol

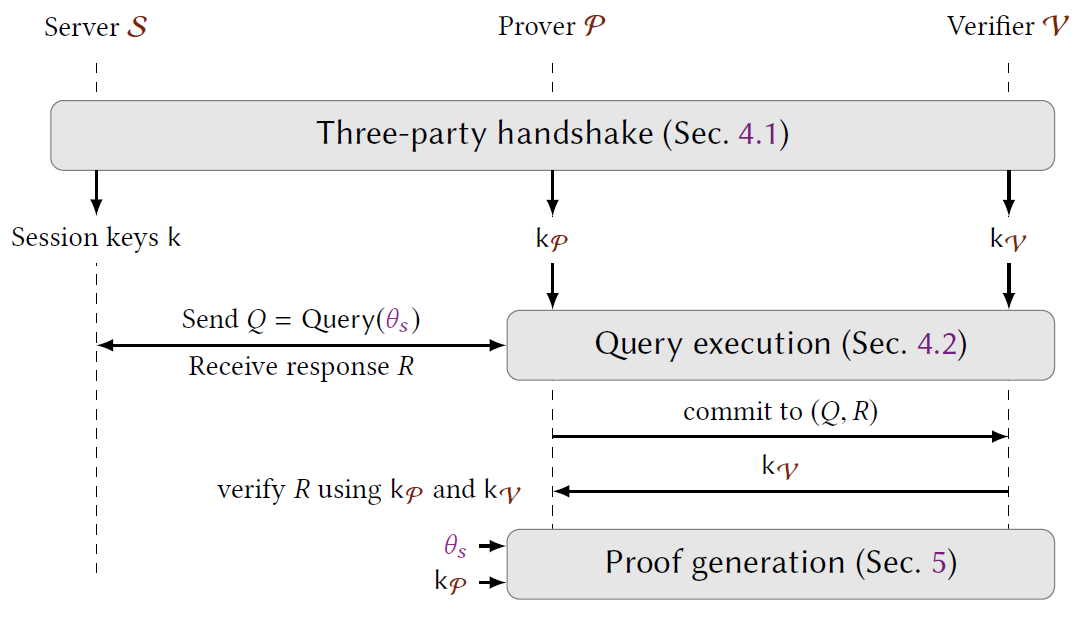
Trigger:

Verifier ( $\mathcal{V}$ ) is asked for off-chain data,

$\mathcal{V}$ generates a session ID ( $sid$ ), a query template ( $Query$ ), and a statement ( $Stmt$ ) to be proven.

$\mathcal{V}$ sends $(sid, Query,Stmt)$ to $\mathcal{P}$ .

Three-party handshake

The goal of the three-party handshake is to run a TLS handshake protocol, which for the server ( $\mathcal{S}$ ) side is just following the standard TLS protocol, but the prover ( $\mathcal{P}$ ) and verifier ( $\mathcal{V}$ ) use a separated key which can be combined to communicate with the server. (All additions and multiplications are Elliptic Curve operations)

$\mathcal{P}$ sends “client hello” to $\mathcal{S}$ , along with TLS type, cipher suite with a random $r_c$ generated by $\mathcal{P}$ .

$\mathcal{S}$ receives the data, sends “server hello” to $\mathcal{P}$ , along with certificate $cert$ , cipher suite with a random $r_s$ generate by the server, and server’s public key $Y_S$ and a signature $\mathcal{\sigma}$ over $(r_c, r_s, Y_S)$ .

$\mathcal{P}$ verifies that $cert$ is valid and $\mathcal{\sigma}$ is valid over $(r_c, r_s, Y_S)$ , then sends $(r_c, r_s, Y_S,\mathcal{\sigma},cert)$ to $\mathcal{V}$ . Then $\mathcal{V}$ checks the same thing also.

$\mathcal P$ and $\mathcal V$ jointly generate a private key:
1. $\mathcal{V}$ generates a secret $s_v$ , calculates the verifier premaster key $Y_V=s_v*G$ , and sends $Y_V$ to $\mathcal{P}$ .
1. $\mathcal{P}$ generates a secret $s_p$ , calculates the prover premaster key $Y_P=s_p*G$ , runs the key exchange procedure, and sends $Y_P+Y_V$ to $\mathcal{S}$ after encrypting with $Y_S$ .
1. $\mathcal P$ an $\mathcal V$ run $ECtF$ to compute a sharing of x-coordinate of $Y_P+Y_V$ , denoted as $z_P$ and $z_V$ .
  Source: https://arxiv.org/abs/1909.00938
1. $\mathcal P$ and $\mathcal V$ send $z_P$ and $z_V$ to $\mathcal F_{2PC}^{hs}$ (see below figure) to compute $(k^{Enc},r_k,r_m)$ and $(r_k⊕k^{MAC},r_m⊕m)$ , send to $\mathcal P$ and $\mathcal V$ respectively, which is $(k^{Enc},k^{MAC}_{\mathcal{P}},m_{\mathcal{P}})$ and $(k^{MAC}_{\mathcal{V}},m_{\mathcal{V}})$ .
  Source: https://arxiv.org/abs/1909.00938
1. $\mathcal{P}$ computes a hash $h$ of the handshake messages, and runs a 2PC-PRF with $\mathcal{V}$ to compute $s_p=PRF(m_{\mathcal{P}}⊕m_{\mathcal{V}},$ “client finished” $,h)$ , sends to $\mathcal{S}$ .
1. $\mathcal{S}$ computes $s_s=PRF(m_{\mathcal{P}}⊕m_{\mathcal{V}},$ “server finished” $,h)$ , sends it to $\mathcal{P}$ , then $\mathcal{P}$ and $\mathcal{V}$ recompute and check if $s_s=PRF(m_{\mathcal{P}}⊕m_{\mathcal{V}},$ “server finished” $,h)$ , and abort if not. Three-party handshake complete.

Note that at the end of the three-party handshake,

$P$  obtains $k^{MAC}_{P}$  and $k^{Enc}$ ,

$V$  obtains $k^{MAC}_{V}$ .

Query execution

$\mathcal{P}$ constructs the query using the template $Q=Query(θ_s)$ , $θ_s$ is some secret parameter stored in $\mathcal{P}$ , e.g. API key, password, etc.

$\mathcal{P}$ invokes 2PC-HMAC with $\mathcal{V}$ to compute a tag $\mathcal{τ}$ which signs the query message $Q$ , sends $(sid, \hat{Q}=Enc(k^{Enc},Q||τ)$ to $\mathcal{S}$ . (The goal of this step is to ensure that the content of the query is not been manipulated by $\mathcal P$ ).
The goal of 2PC-HMAC is to compute $HMAC_H(k^{MAC},m)$ , which is the following equation, where $opad$ is $01011100$ repeated and $ipad$ is $00110110$ repeated.
$HMAC_H(k^{MAC},m)=H((k^{MAC}⊕opad)||H((k^{MAC}⊕ipad)||m))$
1. $\mathcal{P}$ and $\mathcal{V}$ input $k^{MAC}_{\mathcal{P}}$ and $k^{MAC}_{\mathcal{V}}$ to run a 2PC to compute $s_0=f(IV,k^{MAC}⊕ipad)$ , and reveal $s_0$ to $\mathcal{P}$ , where $f$ denotes a compression hash function of SHA256 and $IV$ is an initialization vector. Note that $s_0$ is computed once in a TLS session.
1. $\mathcal{P}$ computes the inner hash $h_i=f(s_0,Q)$ , which represents $H((k^{MAC}⊕ipad)||Q)$ in the above equation.
1. $\mathcal{P}$ inputs $k^{MAC}_{\mathcal{P}}$ , $h_i$ and $\mathcal{V}$ inputs $k^{MAC}_{\mathcal{V}}$ to run a 2PC to compute $H((k^{MAC}⊕opad)||h_i)$ , which outputs $τ$ .

Commit and verify:

$\mathcal{P}$ sends $(sid, \hat{Q}=Enc(k^{Enc},Q||τ)$ to $\mathcal{S}$ .

$\mathcal{S}$ responds to $\mathcal{P}$ with $(sid, \hat R)$ ,
1. $\mathcal{P}$ sends $(sid, \hat R,k^{MAC}_{\mathcal P})$ to $\mathcal{V}$ , (note that now $\mathcal{V}$ has the $\hat{R}$ , so it cannot be altered)
1. then $\mathcal V$ sends back $(sid,k^{MAC}_{\mathcal V})$ .

$\mathcal{P}$ computes $k^{MAC}=k^{MAC}_{\mathcal P}+k^{MAC}_{\mathcal V}$ , decrypts $R||τ=Dec(k^{Enc},\hat R)$ , and verifies $τ$ with $k^{MAC}$

Proof generation

Define $b=Stmt(R)$ which is a statement about the response $R$ (e.g: “Alice has more than $3000 in the bank balance”), $x=(k^{Enc},θ_s,Q,R)$ , $w=(\hat Q, \hat R, k^{MAC},b)$ , $\mathcal{P}$ sends $(sid,``prove",x,w)$ to ZKP function $\mathcal{F}_{ZK}$ .

$\mathcal{F}_{ZK}$ constructs a relation $π(x,w)∈\left\{ {0,1}\right\}$ , which is $1$ if and only if:
1. $\hat Q$ and $\hat R$ are the ciphertexts of $Q$ and $R||τ$ under $k^{Enc}$ and $k^{MAC}$ .
1. $Query(θ_s)=Q$
1. $Stmt(R) = b$

$\mathcal{F}_{ZK}$ sends $(sid,"proof",π,(\hat Q, \hat R, \hat k^{MAC},b))$ to $\mathcal V$ .

$\mathcal V$ checks if $\hat k^{MAC}=k^{MAC}_\mathcal V+k^{MAC}_\mathcal P$ , and verifies the proof $\pi$ .

Assessment

DECO would allow a user to prove, in zero-knowledge, that some information comes from a specific TLS session with a specific server, and further that this information is taken from the right context. If such a tool were implemented, it would be of paramount importance for the transport of Web2 data to Web3. We label it as very relevant.

References

https://arxiv.org/abs/1909.00938

https://eprint.iacr.org/2016/168

https://eprint.iacr.org/2017/578.pdf