In this page we give preliminary information including definitions of the notions that are mostly used in the papers through our database.

Zero-knowledge

Zero-knowledge proof is a protocol in which a party (the prover) proves a statement to another party (the verifier) without revealing anything about what makes the statement true.

Properties of zero-knowledge proofs

Zero-knowledge proofs must have the following properties.

• Completeness means that the proof for a correct statement given by an honest prover should be accepted with probability $1$ by an honest verifier.

• Soundness means that it should be infeasible for a malicious prover to convince the verifier of an incorrect statement. Note that PoKs (Proof of Knowledge) have a stronger soundness property which is called knowledge soundness. This means that if the prover does not know a witness for the statement, then it cannot make the verifier accept a proof for that statement.

• Zero-knowledge means that the proof reveals no information about the prover’s secret input, except the correctness of the statement.

zk-SNARKs

zk-SNARK stands for,

• Zero-Knowledge,

• Succinct, (the proof size is small and easy to verify),

• Non-interactive,

• ARgument of Knowledge.

They are efficient instantiations of NIZKs, which have a wide application spectrum from verifiable computations to the privacy-preserving transfer of funds.

Given a field $\mathbb{F}$, and an $\mathbb{F}$-arithmetic circuit $C : \mathbb{F}^n × \mathbb{F}^h \rightarrow \mathbb{F}^l$ we denote a corresponding language by associated binary relation by $\mathcal{R}_C = \{(x, a) \in \mathbb{F}^n × \mathbb{F}^h \rightarrow \mathbb{F}^l : C(x, a) = 0^l \}$ and a language $\mathcal{L}_C = \{x \in \mathbb{F}^n : \exists a \in \mathbb{F}^h , C(x, a) = 0^l \}$.

A zk-SNARK for $\mathbb{F}$ is a triple of Probabilistic Polynomial Time (PPT) algorithms $(Setup, Prove, Verify)$ as follows:

Signature scheme

Signature schemes are cryptographic protocols that are used to verify the authenticity of a message. Signature schemes use public-key cryptography, i.e. signers have private and public key pairs which are used for signature generation and verification, respectively.

Signature schemes are one of the main parts of verifiable credentials in the W3C’s definition. A verifiable credential may be seen as the signature of an issuer on a set of holder-specific data (id, attributes, etc.).

Below we give a formal definition of a signature scheme.

Definition (Signature scheme)

A signature scheme is a protocol specified by four algorithms $\textsf{PG, KG, Sig, Ver}$ which can be defined as follows:

• $\textsf{PG}(1^{\kappa})\to pp$ is the parameter generation algorithm that takes the security parameter $\kappa$ as input and outputs the public parameters $pp$ which includes hash functions, cyclic groups, generators, etc.

• $\textsf{KG}(pp)\to (sk,pk)$ is the key generation algorithm that takes the public parameters $pp$ as input and outputs a private and public key pair, i.e. $(sk,pk)$.

• $\textsf{Sig}(pp, sk, M) \to \sigma$ is the signature generation algorithm, which takes public parameters $pp$, the private key $sk$, and the message $M$ as inputs, and outputs the signature $\sigma$.

• $\textsf{Ver}(pp, pk, M, \sigma)\to 1/0$ is the verification algorithm that takes public parameters $pp$, public key $pk$, the message $M$ and the signature $\sigma$ as inputs, and outputs $accept/reject$.

Properties of signature schemes

The security of a signature scheme is mainly contained in the unforgeability property which means that for any PPT adversary, it is unfeasible to generate a valid signature on any previously unsigned message, with a non-negligible probability of acceptance. The unforgeability property of a signature scheme depends on the underlying security assumption, for example, the Discrete Logarithm assumption, the Decisional Diffie-Hellman assumption, the RSA assumption, etc.

There exist many types of signature schemes, such as multi-signatures, threshold signatures, ring signatures, group signatures, blind signatures, etc., according to the functionalities that are needed.

Different types of signature schemes may have different properties. For example, consider an anonymous credential scheme. For issuing an anonymous credential, an issuer shouldn’t learn the attributes of the user. Therefore he uses a blind signature scheme in which the signer signs a commitment to the user’s private data. As required in this example a blind signature scheme should have two properties. The first one is blindness which means a signer shouldn’t learn any information about the message he signs. The second one is one-more-unforgeability: a special form of unforgeability in which any user engaging with a signer $\ell$ times shouldn't be able to generate more than $\ell$ signatures on previously unsigned messages.

Cryptographic accumulators

A cryptographic accumulator is a short binding commitment to a set of values. The cryptographic accumulators can be categorized into two classes, i.e. symmetric and asymmetric accumulators.

• Symmetric accumulators are designed with symmetric cryptographic primitives. These designs can verify membership without a witness. (e.g. The Bloom filter [20])

• Asymmetric accumulators are designed on top of the asymmetric cryptographic primitives and they require a witness for verification of set membership.(e.g. RSA accumulator 2017 [21])

Security properties

• Soundness is defined as the probability of computing a membership/non-membership witness for an element that isn’t/is a part of the accumulator is negligible.

• Completeness means that all honestly accumulated values should be verified with non-negligible probability.

• Undeniable means that the probability of generating membership and non-membership witnesses at the same time should be negligible.

• Indistinguishability means that no information about the accumulated set should be leaked by witnesses or accumulators.

Optional properties

Optional properties that a cryptographic accumulator may have can be found in the below table.

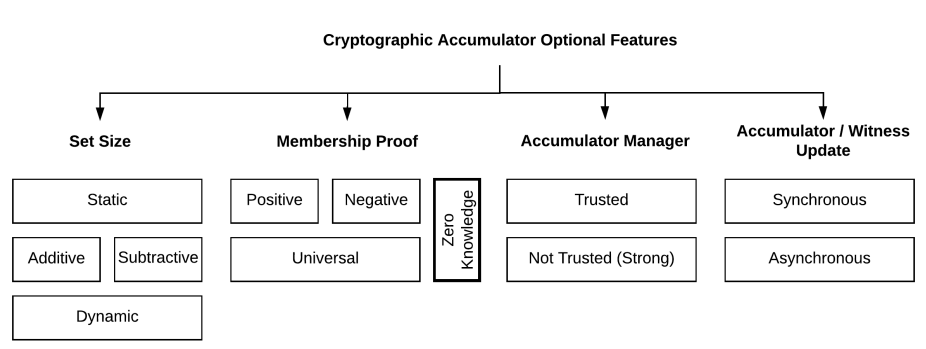
The first set of properties depends on the set size. An accumulator can be additive, subtractive, static, or dynamic according to addition or deletion support it has.

The second set depends on the membership proof. An accumulator can be positive, negative or universal according to the proof type it supports, i.e. membership, non-membership, or both. Note that all these three types can be achieved in zero-knowledge fashion.

The third set depends on the accumulator manager. An accumulator can be trusted or not trusted (or strong) according to the the need for a trusted or not trusted manager.

Finally the fourth set depends on the communication type. An accumulator can be synchronous or asynchronous according to the synchrony assumption it has.

Commitment schemes

A commitment scheme is a cryptographic building block widely used in cryptographic protocols. It enables a user (in a protocol) to choose a value and commit to it in a way that it can no longer be altered. The user doesn’t have to reveal the value that he committed to. However, he can choose to do so if needed.

Definition (Commitment scheme)

A commitment scheme is specified by three algorithms, i.e. $\textsf{KeyGen}$, $\textsf{Com}$, and $\textsf{Ver}$ which can be defined as follows:

• $\textsf{KeyGen}(1^{\kappa})\to ck$ is the key generation algorithm that takes security parameter $\kappa$ as input and outputs a commitment key.

• $\textsf{Com}(m,ck) \to (C,D)$ is the commitment algorithm that takes the value to be committed $m$ and the commitment key $ck$ as inputs and outputs a commitment-opening $(C,D)$ pair.

• $\textsf{Ver}(m,ck,C,D) \to 1/0$ is the verification algorithm that takes the committed value $m$, the commitment key $ck$ and the commitment-opening pair $(C,D)$ as inputs and outputs accept or reject.

Properties of commitment schemes

The security of a commitment scheme is defined over two main properties, i.e. hiding and binding properties.

Hiding property means that after a prover commits to a value, a verifier cannot learn anything about the value unless the prover reveals it.

Binding property means that after a prover commits to a value, he cannot change the value included in the commitment. In other words, when a prover reveals the value by opening a commitment, the verifier knows that the revealed information is the value that was committed to originally.

These properties are usually achieved by using the underlying assumptions such as the RSA assumption, the CDH assumption, etc.

Threshold Public-Key Encryption (TPKE)

Threshold Public-Key Encryption (TPKE) is an extension of public-key encryption where a single party holds the secret decryption key. In TPKE, a number of parties hold partial secret decryption keys (usually generated by distributed key generation protocols), and a sufficient number (threshold) of users can jointly decrypt a ciphertext.

A TPKE scheme can be defined by four algorithms, i.e. $\textsf{TKeyGen, Enc, TDec}$ and $\textsf{Combine}$ that can be defined as follows:

• $\textsf{TKeyGen}(par,n,t)\to pk, \{sk_i\}_{i=1}^{n}$: Threshold key generation algorithm takes system parameters $par$, number of users $n$ and the threshold value $t$ as inputs, and outputs a public key $pk$ and partial secret keys $sk_i$ for $n$ users ($i=1,\dots,n$). This can be achieved by a trusted dealer running a secret sharing scheme, or can be achieved interactively without a trusted party.

• $\textsf{Enc}(pk,m)\to ct$: Encryption algorithm takes the public key $pk$ and the message $m$ as inputs, and outputs the ciphertext $ct$.

• $\textsf{TDec}(ct,sk_i)\to pt_i$: Threshold decryption algorithm takes the ciphertext $ct$ and a partial secret key $sk_i$ as inputs and outputs a partial decryption $pt_i$. Note that this algorithm is run by all available users. If at least $t$ of them obtains a partial decryption they can combine their partial decryptions with the following algorithm.

• $\textsf{Combine}(S,\{pt_i\}_{i\in S})\to m$: Combine algorithm takes a set $S$ of user’s indices with $|S|\geq t$ and the partial decryptions of the users corresponding to the set $S$, and outputs the message.

Bilinear Pairings

Let $G_1$, $G_2$, and $G_t$ be cyclic groups of the same order $p$. A bilinear pairing $\textsf{e}:G_1 \times G_2 \rightarrow G_t$ is a function that maps a pair of elements from groups $G_1$ and $G_2$ to another group, and satisfies the following properties:

• Bilinearity: $\textsf{e}(g_1^a, g_2^b) = \textsf{e}(g_1, g_2)^{ab}$, for all $g_1 \in G_1$ and $g_2 \in G_2$ and $a,b \in \mathbb{F}_p$,

• Non-degeneracy: $\textsf{e}(g_1, g_2) \neq 1$, for all $g_1 \in G_1$ and $g_2 \in G_2$,

• Efficiency: The map $\textsf{e}$ is efficiently computable.

Types of pairings

There exist three basic types of bilinear pairings [12]

1. Type-1: $G_1 = G_2$

2. Type-2: $G_1 \neq G_2$ but there exists an efficient homomorphism $\phi : G_2 \rightarrow G_1$ , while no efficient one exists in the other direction.

3. Type-3: $G_1 \neq G_2$ and no efficiently computable homomorphism exists between $G_1$ and $G_2$, in either direction.

Type-1 pairings (also called symmetric pairings) are insecure since DDH is easy in $G_1$. Type-2 pairings have intermediate efficiency due to the homomorphism from $G_2$ to $G_1$. Type-3 pairings are more efficient than other types. They support the XDH assumption which implies the difficulty of the Computational co-Diffie-Hellman (co-CDH) problem in $G_1$ and $G_2$, and the difficulty of the Decisional Diffie-Hellman (DDH) problem in $G_1$.

Cryptographic Hash Function

A cryptographic hash function maps input strings of an arbitrary length to output strings of fixed length. The hash function is a many-to-one function as the number of inputs is larger than the outputs.

A cryptographic hash function $\textsf{H}$ has the following properties:

• Preimage resistance: Let $y$ be an output of a hash function $\textsf{H}$ with unknown input. Let an input $x$ that satisfies $y = \textsf{H}(x)$ be the preimage of $y$ under $\textsf{H}$. By the many-to-one nature of the $\textsf{H}$, preimages are not necessarily unique. The function $\textsf{H}$ is said to be preimage resistant if it is computationally infeasible to calculate any preimage $x$ of a given $y$.

• Second preimage resistance: Given an input string $x$, it is computationally infeasible to find a different input string $x'$ such that $\textsf{H}(x') = \textsf{H}(x)$.

• Collision resistance: It is computationally infeasible to find two distinct input strings $x$ and $x'$ such that $\textsf{H}(x) = \textsf{H}(x')$.

Decentralized Identity

Definitions related to Decentralized Identity can be found in Decentralized identity, the ultimate guide.

Verifiable credentials

A Verifiable Credential (VC) is a credential with cryptographic proof that an issuer indeed issued the credential for a user and agrees with the user’s claims included in it. Definitions related to Verifiable Credentials can be found in W3C’s Verifiable Credentials Data Model v1.1.

Sybil resistance

A Sybil attack is a kind of attack against a network in which the attacker gains disproportionately large influence on the network by creating multiple identities and submitting them to the system. For example, consider a threshold signature scheme used in a distributed network. If the number of identities that the attacker holds is more than the threshold, then it can produce valid signatures on any message on behalf of the entire network.

It is crucial for a distributed system to have a sufficient level of Sybil resistance. For example, a Sybil resistance mechanism could rely on

• identity validation (using central authorities for validating the identity of the user)

• social trust graph algorithms (based on the connectivity characteristics of social graphs)

• economic costs (exposing the users to an economic cost during registration or use, such as Proof-of-Work systems )

• personhood validation (CAPTCHA-like measures)

References

1. Decentralized Anonymous Credentials, https://eprint.iacr.org/2013/622.pdf.

2. ZEBRA: Anonymous Credentials with Practical On-chain Verification and Applications to KYC in DeFi, https://eprint.iacr.org/2022/1286.

3. Efficient Sparse Merkle Trees Caching Strategies and Secure (Non-)Membership Proofs, https://eprint.iacr.org/2016/683.

4. Proofs that yield nothing but their validity and a methodology of cryptographic protocol design, https://ieeexplore.ieee.org/document/4568209.

5. An Efficient Threshold Public Key Cryptosystem Secure Against Adaptive Chosen Ciphertext Attack, https://link.springer.com/content/pdf/10.1007/3-540-48910-X_7.pdf

6. Threshold Signatures, Multisignatures and Blind Signatures Based on the Gap-Diffie-Hellman-Group Signature Scheme, https://link.springer.com/content/pdf/10.1007/3-540-36288-6_3.pdf

7. Security of Blind Signatures Revisited, https://link.springer.com/content/pdf/10.1007/s00145-015-9225-1.pdf.

8. Commitment Schemes and Zero-Knowledge Protocols, https://www.researchgate.net/publication/221621428_Commitment_Schemes_and_Zero-Knowledge_Protocols

9. Verifiable Credentials Data Model v1.1, https://www.w3.org/TR/vc-data-model/

10. Decentralized Identifiers (DIDs) v1.0, https://www.w3.org/TR/did-core/

11. https://en.wikipedia.org/wiki/Sybil_attack.

12. Pairings for Cryptographers, https://eprint.iacr.org/2006/165.

13. An Introduction to Pairing-Based Cryptography, https://www.math.uwaterloo.ca/~ajmeneze/publications/pairings.pdf.

14. Discrete Logarithm Problem, https://en.wikipedia.org/wiki/Discrete_logarithm

15. Decisional Diffie-Hellman Assumption, https://en.wikipedia.org/wiki/Decisional_Diffie–Hellman_assumption

16. RSA Problem, https://en.wikipedia.org/wiki/RSA_problem

17. Efficient Revocation of Anonymous Group Membership Certificates and Anonymous Credentials, https://eprint.iacr.org/2001/113.pdf.

18. Universal Accumulators with Efficient Nonmembership Proofs, https://www.cs.purdue.edu/homes/ninghui/papers/accumulator_acns07.pdf

19. An Overview of Cryptographic Accumulators, https://arxiv.org/pdf/2103.04330.pdf

20. Bloom, B. H. (1970a). Space/time trade-offs in hash coding with allowable errors. Comm. of the ACM, 13(7):422–426. https://dl.acm.org/doi/10.1145/362686.362692

21. Baldimtsi, F., Camenisch, J., Dubovitskaya, M., Lysyanskaya, A., Reyzin, L., Samelin, K., and Yakoubov, S. (2017). Accumulators with applications to anonymity-preserving revocation. In 2017 IEEE European Symp. on Security & Privacy (EuroS&P), pages 301–315. IEEE, https://www.researchgate.net/publication/318125384_Accumulators_with_Applications_to_Anonymity-Preserving_Revocation

22. XDH assumption, https://en.wikipedia.org/wiki/XDH_assumption

23. Computational Diffie–Hellman assumption, https://en.wikipedia.org/wiki/Computational_Diffie–Hellman_assumption