The Sybil Attack
| Abstract | Large-scale peer-to-peer systems face security threats from faulty or hostile remote computing elements. To resist these threats, many such systems employ redundancy. However, if a single faulty entity can present multiple identities, it can control a substantial fraction of the system, thereby undermining this redundancy. One approach to preventing these “Sybil attacks” is to have a trusted agency certify identities. This paper shows that, without a logically centralized authority, Sybil attacks are always possible except under extreme and unrealistic assumptions of resource parity and coordination among entities. |
|---|---|
| Year | 2002 |
| Link to the paper | https://www.microsoft.com/en-us/research/wp-content/uploads/2002/01/IPTPS2002.pdf |
| Relevance score | Very relevant |
| Quality score | 4 |
| Labels | Classic referenceSybil resistance insights |
This is the seminal paper defining the notion of a Sybil attack. It also alludes to some nice impossibility results, regarding the difficulties of validating separate identities via “proof of resources”.
Section 1: Introduction
It is tempting to envision a system in which established identities vouch for other identities, so that an entity can accept new identities by trusting the collective assurance of multiple (presumably independent) signatories, analogous to the PGP web of trust [37] for human entities. However, our results show that, in the absence of a trusted identification authority (or unrealistic assumptions about the resources available to an attacker), a Sybil attack can severely compromise the initial generation of identities, thereby undermining the chain of vouchers.
Section 2: formal model
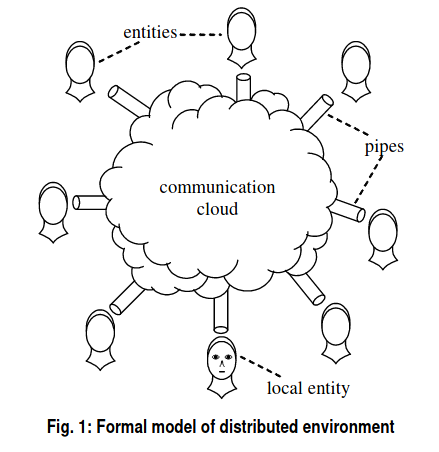
- Partition the set of entities into (correct) and (faulty, byzantine)
- Entities communicate via messages broadcasted to the cloud. All messages are guaranteed to eventually be delivered to all entities. (I.e. we neglect DDOS or eclipse attacks)
- Our model excludes direct links between entities because a physical link provides a form of centrally supplied identification of a distinct remote entity.
- Entities vs identities: An identity is an abstract representation that persists across multiple communication events. Each entity attempts to present an identity i to other entities in the system. If e successfully presents identity i to l, we say that l accepts identity i.
- Each correct entity c will attempt to present one legitimate identity. Each faulty entity f may attempt to present a legitimate identity and one or more counterfeit identities.
Section 3: results
Three ways to validate an identity:
- A trusted, centralized source
- Directly (by oneself)
- Indirectly (by trusting the validation of already-accepted identities)
We will show the following 4 lemmas:
For direct validation, we show:
- Even when severely resource-constrained, a faulty entity can counterfeit a constant number of multiple identities.
- Each correct entity must simultaneously validate all the identities it is presented; otherwise, a faulty entity can counterfeit an unbounded number of identities.
- This is a direct impediment to scalability.
- Comment: validate identities at regular, scheduled times to facilitate this? The problem is that malicious entities can “rent” resources only to bypass the challenges.
For indirect validation, we show:
- A sufficiently large set of faulty entities can counterfeit an unbounded number of identities.
- This places a limit on system size (since we should assume the number of faulty entities will scale proportionally)
- All entities in the system must perform their identity validations concurrently; otherwise, a faulty entity can counterfeit a constant number of multiple identities.
- Harder to satisfy as system size increases.
Direct identity validation
If we assume that the resources of any two entities differ by at most a constant factor (i.e. there is a minimum amount of acceptable resources to participate of the network), a local entity can demand proof of a remote entity’s resources before accepting its identity.
However, this leaves us with the following limitation:
Examples of this “proof of resources”:
- Communication resources: local entity can broadcast a request for identities and then only accept replies that occur within a given time interval.
- Storage resources: entity can challenge each identity to store a large amount of unique, uncompressible data. By keeping small excerpts of this data, entity can verify, with arbitrarily high probability, that all identities simultaneously store the data they were sent.
- Computation resources: entity can challenge each identity to solve a unique computational puzzle. (Proof-of-work)
To be effective, these resource challenges must be issued to all identities simultaneously:
Indirect identity validation
In addition to accepting identities that it has directly validated using one of the challenge mechanisms described above, an entity might also accept identities that have been validated by a sufficient count of other identities that it has already accepted.
An obvious danger of accepting indirectly validated identities is that a group of faulty entities can vouch for counterfeit identities:
Thus, multiple entities need to issue their challenges concurrently.
Like Lemma 1, the result of Lemma 4 is that a faulty entity can amplify its influence. A system that can tolerate a fraction φ of all identities being faulty can tolerate only φ/g of all entities being faulty. In some systems, this may be acceptable.