Coconut: Threshold Issuance Selective Disclosure Credentials with Applications to Distributed Ledgers

About Coconut

Coconut is a selective disclosure credential scheme that supports:

• Distributed threshold issuance

• Public and private attributes

• Re-randomization - protecting privacy even in the case in which all authorities and verifiers collude

• Multiple unlinkable selective attribute revelations

Overview of Coconut

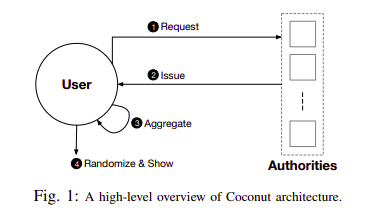
1. Any Coconut user may send a Coconut request command to a set of Coconut signing authorities; this command specifies a set of public or encrypted private attributes to be certified into the credential.

2. Each authority answers with an issue command delivering a partial credential.

3. Any user can collect a threshold number of shares, aggregate them to form a single consolidated credential and re-randomize it.

4. The user who owns the credentials can then execute the show protocol to selectively disclose attributes or statements about them. The showing protocol is publicly verifiable and may be publicly recorded.

The design Goals of Coconut

1. Threshold authorities: Only a subset of the authorities is required to issue partial credentials in order to allow the users to generate a consolidated credential. The communication complexity of the request and issue protocol is $\mathcal{O}(t)$. Where $t$ is the subset of authorities.

2. Non-interactivity: The authorities may operate independently of each other, i.e., following a simple key distribution and setup phase, they do not need to synchronize or further coordinate their activities.

3. Blindness: The authorities issue the credential without learning any additional information about the private attributes included in the credential.

4. Unlinkability: It is impossible to link multiple showings of the credentials with each other, or the issuing transcript, even if all the authorities collude.

5. Liveness: Coconut guarantees liveness as long as the threshold number of authorities is honest.

6. Efficiency: After aggregation and re-randomization, the attribute showing and verification involve only a single consolidated credential, and are therefore $\mathcal{O}(1)$ in terms of both cryptographic computations and communication of cryptographic material.

7. Short credentials: Each partial credential and the consolidated credential is composed of exactly two group elements, no matter the number of authorities or the number of attributes embedded in the credentials.

Cryptographic primitives

1. Zero-knowledge proofs: $NIZK\{(x, y, \dots ) : statements \hspace{0.1cm} about \hspace{0.1cm} x, y, \dots\}$

2. Bilinear-map: Coconut requires groups $(\mathbb{G_1} , \mathbb{G_2} , \mathbb{G_T})$ of prime order $p$ with a bilinear map $e : \mathbb{G_1} \times \mathbb{G_2} \rightarrow \mathbb{G_T}$ satisfying Bilinearity and non-degeneracy properties.

3. A cryptographically secure hash function $H : \mathbb{G_1} \rightarrow \mathbb{G_1}$.

Coconut scheme definition

• Setup$(1^\lambda) \rightarrow (params)$: defines the system parameters $params$ with respect to the security parameter $\lambda$. These parameters are publicly available.

• KeyGen$(params) \rightarrow (sk, vk)$: is run by the authorities to generate their secret key $sk$ and verification key $vk$ from the public $params$.

• AggKey$(vk_1 ,\dots, vk_t) \rightarrow (vk)$: is run by whoever wants to verify a credential to aggregate any subset of $t$ verification keys $vk_i$ into a single consolidated verification key $vk$. AggKey needs to be run only once.

• IssueCred$(m, \phi) → (\sigma)$: is an interactive protocol between a user and each authority, by which the user obtains a credential $\sigma$ embedding the private attribute $m$ satisfying the statement $\phi$.

• AggCred$(\sigma_1 , . . . , \sigma_t) \rightarrow (\sigma)$: is run by the user to aggregate any subset of $t$ partial credentials $\sigma_i$ into a single consolidated credential $\sigma$.

• ProveCred$(vk, m, \phi') \rightarrow (\Theta, \phi')$: is run by the user to compute a proof $\Theta$ of possession of a credential certifying that the private attribute $m$ satisfies the statement $\phi'$.

• VerifyCred$(vk, \Theta, \phi') → (true/f alse)$: is run by whoever wants to verify a credential embedding a private attribute satisfying the statement $\phi'$ , using the verification key $vk$ and cryptographic material $\Theta$ generated by ProveCred.

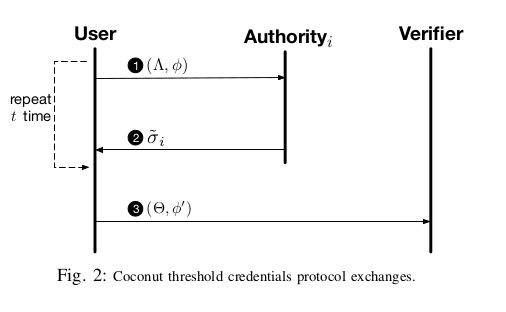
The Coconut Threshold Credential Scheme construction

The Coconut threshold credential scheme allows users to obtain a partial credential $σ_i$ on a private or public attribute $m$. In a system with $n$ authorities, a $t$-out-of-$n$ threshold credentials scheme offers great flexibility as the users need to collect only $n/2 < t \leq n$ of these partial credentials in order to recompute the consolidated credential (both $t$ and $n$ are scheme parameters).

• Setup$(1^\lambda) \rightarrow (params)$: Choose a bilinear group $(\mathbb{G_1} , \mathbb{G_2} , \mathbb{G_T})$ with order $p$ ($\lambda$-bit prime number). Let $g_1 , h_1$ be generators of $\mathbb{G_1}$ , and $g_2$ a generator of $\mathbb{G_2}$ . The system parameters are $params = (\mathbb{G_1} , \mathbb{G_2} , \mathbb{G_T} , p, g_1 , g_2 , h_1 )$.

• TTPKeyGen$(params, t, n) \rightarrow (sk, vk)$: Pick two polynomials $v, w$ of degree $t-1$ with coefficients in $F_p$ , and set $(x, y) = (v(0), w(0))$. Issue to each authority $i \in [1, \dots, n]$ a secret key $sk_i = (x_i , y_i ) = (v(i), w(i))$, and publish their verification key $vk_i = (g_2 , α_i , β_i ) = (g_2 , g_2^{x_i} , g_2^{y_i} )$.

This algorithm is executed by a trusted third-party or distributed key generation (DKG) scheme.

• IssueCred$(m, \phi) → (\sigma)$: Credentials issuance is composed of three algorithms:
  • PrepareBlindSign$(m, \phi) → (d, \Lambda, \phi)$: The users generate an El-Gamal key-pair $(d, γ = g_1^d )$; pick a random $o \in F_p$ , compute the commitment $c_m$ and the group element $h \in \mathbb{G_1}$ as follows:

  $$c_m = g_1^m h_1^o \hspace{0.5cm} and \hspace{0.5cm} h = H(c_m)$$

  Pick a random $k \in F_p$ and compute El-Gamal encryption of $m$ as below:

  $$c = Enc(h^m ) = (g_1^k , \gamma^k h^m )$$

  Output $(d, \Lambda = (γ, c_m , c, π_s ), \phi)$, where $\phi$ is an application-specific predicate satisfied by m, and $\pi_s$ is defined by:

  $$π_s=NIZK\{(d, m, o, k): γ = g_1^d ∧ c_m = g_1^m h_1^o ∧ c = (g_1^k , \gamma^k h^m ) ∧ \phi(m) = 1\}$$

  • BlindSign$(sk_i , \Lambda, \phi) \rightarrow (\tilde{\sigma_i} )$: The authority $i$ parses $Λ = (\gamma, c_m , c, π_s ), sk_i = (x_i , y_i )$and $c = (a, b)$. Recompute $h = H(c_m)$. Verify the proof $\pi_s$ using $\gamma$, $c_m$ and $\phi$; if the proof is valid, build $\tilde{c_i} = (a^{y_i} , h^{x_i}b^{y_i} )$ and output $\tilde{\sigma_i} = (h, \tilde{c_i} )$; otherwise output $\perp$ and stop the protocol.
  • Unblind$(\tilde{\sigma_i} , d) \rightarrow (\sigma_i)$: The users parse $\tilde{\sigma_i} = (h, \tilde{c_i} )$ and $\tilde{c} = (\tilde{a}, \tilde{b})$; compute $\sigma_i = (h, \tilde{b}(\tilde{a})^{−d} )$. Output $σ_i$.

• AggCred$(\sigma_1, \dots, \sigma_t ) \rightarrow Q(\sigma)$: Parse each $σ_i$ as $(h, s_i)$ for $i ∈ [1,\dots, t]$. Output $(h, \prod_{i=1}^{t}s_i^{l_i})$, where $l_i$ is the Lagrange coefficient:

• ProveCred$(vk, m, \sigma, \phi)→ (\Theta, \phi' )$: Parse $σ = (h, s)$ and $vk = (g_2 , \alpha, \beta)$. Pick at random $r' , r ∈ F_p^2$ ; set $σ' = (h' , s') = (h^{r'} , s^{r'})$; build $κ = αβ^m g_2^r$ and $ν = (h')^{r}$ . Output $(Θ = (κ, ν, σ , π_v ), \phi')$, where $\phi'$ is an application-specific predicate satisfied by $m$, and $π_v$ is: $π_v = NIZK\{(m, r) : κ = αβ^m g_2^r ∧ ν = (h')^r ∧ \phi' (m) = 1\}$

• VerifyCred$(vk, \Theta, \phi') \rightarrow (true/f alse)$: Parse $Θ = (κ, ν, σ , π_v )$ and σ' = (h' , s'); verify $\pi_v$ using $vk$ and $\phi'$. Output true if the proof verifies, $h' \neq 1$ and $e(h' , κ) = e(s' ν, g_2 )$; otherwise output false.

Implementation

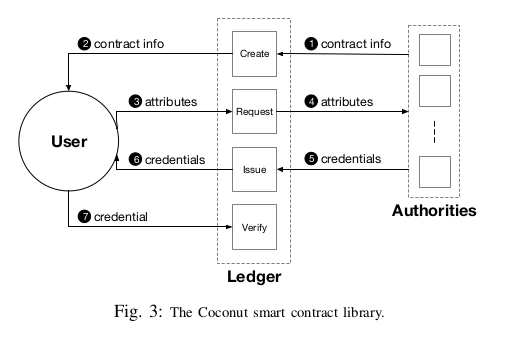
The smart contract has four functions, (Create, Request, Issue, Verify), as illustrated in the above Figure.

1. First, a set of authorities call the Create function to initialize a Coconut instance defining the contract info; i.e., their verification key, the number of authorities, and the threshold parameter.

2. The initiator smart contract can specify a callback contract that needs to be executed by the user in order to request credentials; e.g., this callback can be used for authentication.

3. Any user can request a credential through the Request function by executing the specified callback contract and providing the public (clear texts) and private attributes to include in the credentials.

4. Each signing authority monitors the blockchain at all times, looking for credential requests. If the request appears on the blockchain (i.e., a transaction is executed), it means that the callback has been correctly executed.

5. Each authority issues a partial credential on the specified attributes by calling the Issue procedure.

6. In this implementation, all partial credentials are in the blockchain; however, these can also be provided to the user off-chain. Users collect a threshold number of partial credentials and aggregate them to form a full credential.

7. Then, the users locally randomize the credential. The last function of the Coconut library contract is Verify which allows the blockchain —and anyone else— to check the validity of a given credential.

Limitation: It is not efficient for the authorities to continuously monitor the blockchain.

• Authors implement a smart contract library in Chainspace to enable other application-specific smart contracts to conveniently use our cryptographic primitives.

• The authors also implement an Ethereum smart contract library in solidity. This library is written using Ethereum’s pre-compiled smart contract for point addition and scalar multiplication in $\mathbb{G_1}$, whereas Coconut requires operations on $\mathbb{G_2}$ to verify credentials. The authors also implemented addition and scalar multiplication on $\mathbb{G_2}$ as an Ethereum smart contract library.

• Integration of Coconut into Hyperledger Fabric —a permissioned blockchain platform— is straightforward. Fabric contracts run on private sets of computation nodes—and use the Fabric protocols for cross-contract calls. In this setting, Coconut issuing authorities can coincide with the Fabric smart contract authorities.

Applications

1. Coin Tumbler

2. Privacy-preserving petition

3. Censorship-resistant distribution of proxies

Privacy-preserving petition

Authors consider the scenario where several authorities managing the country $C$ wish to issue some long-term credentials to its citizens to enable any third party to organize a privacy-preserving petition. There are three parties in this system:

1. A set of signing authorities representing $C$

2. The citizens of $C$

3. A petition initiator

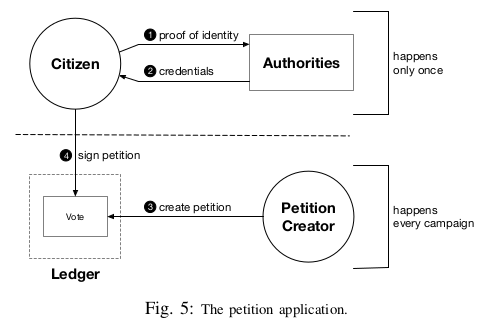
The signing authorities create an instance of the Coconut smart contract as described in the implementation section.

1. The citizen provides a proof of identity to the authorities.

2. The authorities check the citizen’s identity and issue a blind and long-term signature on her private key $k$. This signature, which the citizen needs to obtain only once, acts as her long-term credential to sign any petition.

3. Any third party can create a petition by creating a new instance of the petition contract and become the “owner” of the petition.
   1. The petition instance specifies an identifier $g_s \in \mathbb{G_1}$ unique to the petition
   2. $g_s$ is unlinkable to the other points of the scheme, as well as the verification key of the authorities issuing the credentials and any application-specific parameters (e.g., the options and current votes).
   3. This identifier can be generated through a hash function $F_p \rightarrow \mathbb{G_1}:H(s) = g_s | s \in F_p$.

4. In order to sign a petition,
   1. The citizens compute a value $\zeta = g_s^k$, $k$ is the attribute used in the credential issuance.
   2. They then adapt the zero-knowledge proof of the ProveCred algorithm of construction to show that $\zeta$ is built from the same attribute $k$ in the credential.
   3. The petition contract checks the proofs and the credentials and checks that the signature is fresh by verifying that $\zeta$ is not part of a spent list.
   4. If all the checks pass, it adds the citizens’ signatures to a list of records and adds $\zeta$ to the spent list to prevent a citizen from signing the same petition multiple times (prevent double spending).

Remarks

1. Threshold issuance of credentials through smart contracts and the scheme also supports blindness, unlinkability, and aggregability.

2. On-chain verification of the credentials by two elliptic curve pairings checks.

3. Limitations:
   • Implementing the Coconut smart contract library on Ethereum is expensive as Ethereum does not provide pre-compiled contracts for elliptic curve arithmetic in $G_2$.
   • Adding and removing authorities implies to re-run the key generation algorithm for the threshold signature scheme.

References

1. Coconut: Threshold Issuance Selective Disclosure Credentials with Applications to Distributed Ledgers, https://arxiv.org/pdf/1802.07344.pdf.