CanDiD
| Abstract | We present CanDID, a platform for practical, user friendly realization of decentralized identity, the idea of empowering end users with management of their own credentials. While decentralized identity promises to give users greater control over their private data, it burdens users with management of private keys, creating a significant risk of key loss. Existing and proposed approaches also presume the spontaneous availability of a credential-issuance ecosystem, creating a bootstrapping problem. They also omit essential functionality, like resistance to Sybil attacks and the ability to detect misbehaving or sanctioned users while preserving user privacy. CanDID addresses these challenges by issuing credentials in a user-friendly way that draws securely and privately on data from existing, unmodified web service providers. Such legacy compatibility similarly enables CanDID users to leverage their existing online accounts for recovery of lost keys. Using a decentralized committee of nodes, CanDID provides strong confidentiality for user’s keys, real-world identities, and data, yet prevents users from spawning multiple identities and allows identification (and blacklisting) of sanctioned users. We present the CanDID architecture and its technical innovations and report on experiments demonstrating its practical performance. |
|---|---|
| Year | 2020 |
| Link to the paper | https://www.arijuels.com/wp-content/uploads/2020/07/Candid.pdf |
| Relevance score | Very relevant |
| Quality score | 5 |
| Labels | Legacy compatibleManagement of credentialsSybil resistance insights |
TL;DR
CanDID attempts to address four main issues in decentralized identity:
- Legacy Compatibility
- Sybil resistance
- Accountability
- Key recovery
In the identity system for Lido, CanDID will play a key role in Sybil-resistance. In other words, CanDID would try to ensure that an operator does not try to act as more than one operator to accrue more rewards. The idea of accountability and key recovery may also be useful but only after some modifications (this is because if we use the system for maintaining accountability and key recovery as is, then the dependency on the CanDID committee is huge.).
Short description
- Identity System: CanDID uses services such as DECO or Town Crier to port identities and credentials from web services. These services enable the users to generate trustworthy credentials without issuers generating credentials for them.
- Credential Privacy:
- Selective disclosure - using zero-knowledge arguments.
- Membership privacy - committee members and web service providers cannot obtain the identity of the users as well as the membership of the user (if the user is using CanDID or not).
- Pairwise credentials - CanDID enables users to use different credentials for different services and the credential is unlinkable to any other credential for another service.
- Sybil Resistance: Supports deduplication of identities using a privacy-preserving MPC method.
- Accountability: CanDID can screen users of the system so as to identify the identity of the suspect user. This functionality is privacy-preserving and the committee uses fuzzy matching for finding the identity.
- Credential Privacy:
- Key Recovery System: Leverage existing web authentication schemes to recover keys. Users may store the keys in their local devices and backup with the CanDID committee, prespecify recovery accounts on the web services, and define the recovery policy. To recover the keys, a user has to prove successful logins based on the recovery policy.
Oracles
An oracle relays and provides assurance that the retrieved data is authentic. It allows users to prove that the origin of the data is authentic. CanDID uses oracles to allow users to pull data from existing systems. CanDID proposes that either DECO or Town Crier can be used for this purpose.
System Overview
Identity System
Goal: To convert already existing legacy data to decentralized identity.
CanDID relies on decentralized oracles such as DECO or Town Crier to port credentials from legacy web services. The CanDID committee acts as the verifier for the ported data.
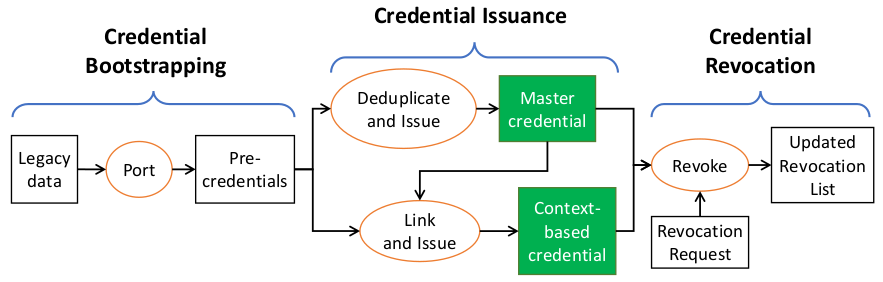
CanDID pulls data from web services using oracles to create credentials. A committee called the “CanDID Committee” acts as the verifier for the data ported.
There are four common requirements: uniqueness, non-transferability, accountability, and privacy.
- Uniqueness and Non-transferability: Uniqueness implies the inclusion of mechanisms to ensure the deduplication of user identities. Non-transferability refers to the integration of preventive measures that prevent users from transferring credentials.
CanDID achieves uniqueness and non-transferability by making the system Sybil-resistant. Sybil resistance is achieved by deduplicating based on one or more attributes. To achieve deduplication, the CanDID committee maintains a secret-shared table of attributes (attributes such as SSNs or Aadhar numbers which are unique to every person). The steps in joining of a new user:
- The user presents one or more pre-credentials asserting various attributes. A pre-credential refers to a credential that has not been deduplicated in CanDID.
- After this, the CanDID committee performs a privacy-preserving MPC deduplication protocol to check the table if the attributes presented in the pre-credential exist. Once it’s confirmed that the attributes presented are unique, then the system issues a master credential.
Making the system Sybil-resistant helps discourage credential transfer.
- Each user can obtain only one master credential in CanDID, disincentivizing sale or transfer.
- Other deterrents such as
- temporary revocation of misused credentials, and
- revocation of stolen credentials
can be effective for the same reason.
CanDID focuses only on truly unique identifiers for deduplication - SSNs, Aadhar number, etc. For the countries that do not have such a unique identifier - they have proposed another method that would prevent the dependency on unique identifiers (discussed later).
The master credential may not contain all attributes for all use cases. Therefore, a user can add more credentials for this purpose. This credential has to be related to the master credential (because it has to be for some person). To do this, the user has to put some information in the context-based credential that is common with the master credential.
- Accountability: CanDID enables the identification of malicious users based on their real-world identities and permits the subsequent listing of such users on a committee-maintained public revocation list. Any verifying party can check this list to see if a user’s credential has been revoked. CanDID supports pulling data from real-world revocation lists as well as handling the case where a user is added newly to the revocation lists.
- Privacy: Privacy is one of the major properties of CanDID.
- Users’ attributes are hidden from committee nodes.
- Attribute-membership privacy: committee members cannot determine if a credential containing a certain attribute exists in the system.
Key Recovery System
Goal: Prevent identity loss
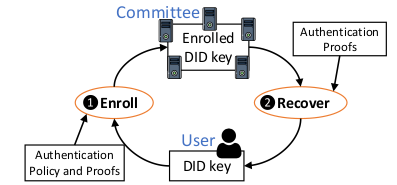
For key recovery - a user provides the key along with a recovery policy. The CanDID committee stores the key in a privacy-preserving manner and releases it when the user meets the criteria mentioned in the recovery policy.
System Model
Three main parties: users, credential issuers, and credential verifiers. CanDID supports the use of DID by relying on a PKI-like architecture where a mapping between DIDs and public keys is stored. The CanDID committee acts as the credential issuer. The CanDID committee stores a joint private key-public key pair. The private key is used for issuing credentials and the public key is used for verifying credentials.
Credential: CanDID uses the W3C specifications for structuring the credential.
A credential contains the following parameters:
| User Identifier () | Pseudonymous identifier of subject of the credential. Also referred to as pseudonym. |
| Context () | Denotes the circumstances where credential is used. |
| Claims () | where, 1. represents the attribute that tells what the claim is about. 2. represents the value of the attribute. 3. represents the provider which denotes the legacy web provider. |
| Signature () | Signature by the issuer |
If there are claims, then and , where is the secret key generated by the CanDID issuer committee. The representation is very similar to the W3C specification. The only difference is the inclusion of the providers in the claim. Each credential contains a property which depicts the attribute used for deduplication. The figure depicts how a credential looks like in CanDID (note that they have used JSON).
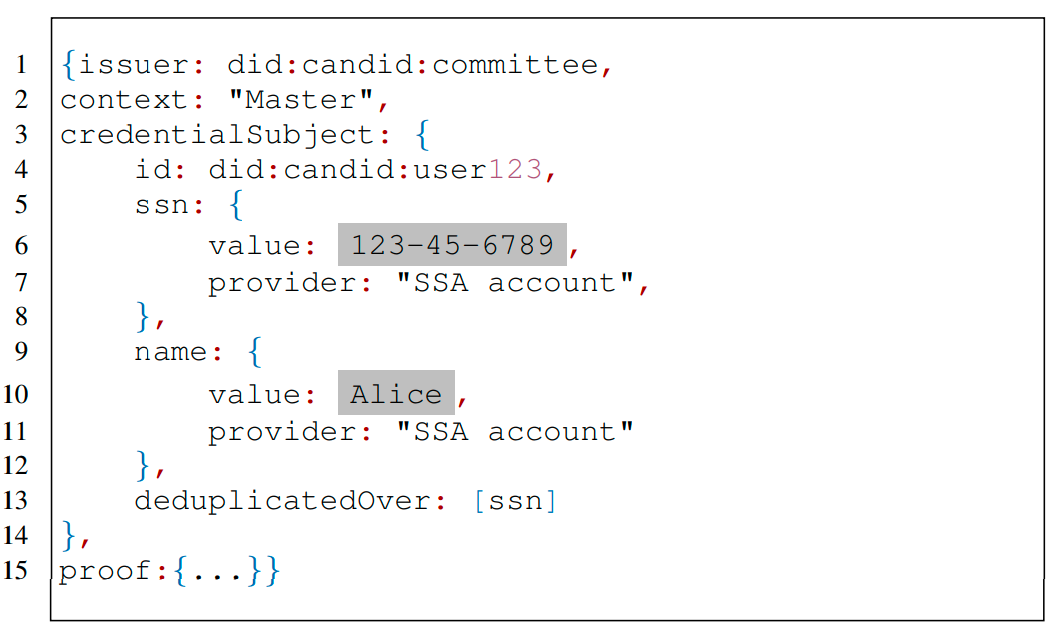
Security Model
Adversarial Model:
Adversary can corrupt up to out of committee nodes, where . The adversary can corrupt any number of users and applications. CanDID committee nodes hold a -Shamir secret sharing of the private key .
Communication Model:
The communication in the network is asynchronous. However, the DKG needed for generation requires weak synchrony in the network for liveness.
Security Properties:
CanDID aims to satisfy certain security properties (since these are definitions, they have been put here as is):
- Sybil resistance: An adversary cannot obtain credentials associated with a larger number of distinct identities than the number of users which are controlled by the adversary.
- Unforgeability: An adversary cannot forge the credentials of the honest user or impersonate them.
- Privacy in Credential issuance and key recovery: It is infeasible for an adversary to learn about the attributes from observation of credential issuance and key recovery.
- Credential Validity: An adversary can obtain credentials only for real-world identities it controls.
- Unlinkability: The entities that deploy applications using CanDID cannot collude and link the respective transactions of any given user. This definition applies only in a weakened adversarial model that rules out malicious committee nodes.
- Privacy in Credential verification: An adversary can learn about a user no more than the information presented by the user using their credentials.
Assumptions on users’ legacy credentials: Some of the security properties depend on some assumptions.
- The credential validity property assumes that an adversary can corrupt as many users as he wants but cannot obtain the credentials of users who haven’t been corrupted.
- The Sybil resistance property assumes that each user has a unique identifier.
Identity System
This system converts legacy data to verifiable credentials. This is done in two steps.
- CanDID converts a set of pre-credentials to a master credential using a privacy-preserving, deduplication protocol. A user has only one master credential and the user does not use this credential with applications.
- Users create context-based credentials which are created for corresponding applications. Context-based credentials are created in a way that they cannot be linked to extract more information about a user.
From legacy data to pre-credentials
A pre-credential is defined as:
where and is the proof for the claim which depicts that the is indeed the value corresponding to the attribute according to the provider . Pre-credentials are used for the creation of both master credentials and context-based credentials. CanDID uses Town Crier or DECO for creating pre-credentials:
- DECO: Here, is the signature over the claim made by the CanDID Committee.
- The user picks at least out of committee members () who would verify the claim and proof generated by DECO ( is the threshold required in the threshold signature scheme used for generating the ).
- Each committee member selected by the user verifies the proof generated by DECO and therefore, the committee member is convinced that the claim generated is authentic.
- Then, committee member generates the partial proof .
- obtains by combining .
- Town Crier: Here, a TEE is used to obtain , which is generated only if the claim is authentic.
To prevent replay attacks, users associate their with the . (such as )
Master credential issuance
Deduplication: CanDID committee stores registered users’ attributes in a table which is called the .
- presents a set of pre-credentials () to the committee.
- The committee checks if matches any entry in the .
- If no information is there, then the committee issues a master credential and adds the user information to the .
- Deduplication Process:
In CanDID, we have to use some attributes using which deduplication can be done. The authors have achieved this by using unique identifiers such as SSNs. This method provides strong Sybil-resistance within a given population. Each committee node stores locally , where is a unique identifier and is a secret key distributed across committee members. When a new user wants to join CanDID, the committee members evaluate and check if is inside the . If it is not present, then a master credential for is created. To ensure that the committee members do not learn about the value , is evaluated using MPC (discussed later).
A limitation of this approach is that it requires users to have unique identifiers which might not be present in many countries. Another way of doing it is by obtaining deduplication parameters using common identifiers such as names and addresses. In addition, this approach poses some threats when implemented. For example, if the system needs multiple pre-credentials from the user for accepting an attribute, then this provides an opportunity for an adversary to compromise multiple accounts of a user.
- Protocol Details: is the attribute over which deduplication has been done.
- System Setup:
- nodes -
- Committee members use a threshold signature scheme
- This scheme generates where and . Each of the nodes knows and . For the secret key, committee member holds and where these keys form a share of the corresponding secret keys.
- Each committee node initializes a local table .
- denotes a sharing of and has such that , where depicts the Lagrange’s coefficients.
- depicts the MPC evaluation of over secret-shared input .
- CanDID uses a secure MPC protocol based on Beaver triples to evaluate .
- Committee generates secret-shared random blinding factors and commitments .
- They have used MP-SPDZ framework for implementation.
- Pre-credential generation: Let denote the ideal value for for . Let , where is a commitment to with a witness .
generates a pre-credential .
- Deduplication: Next step is to evaluate :
- sends to committee members.
- Committee members send shares of a fresh blinding factor to from which reconstructs .
- blinds by: and a proof of correct blinding
sends to all committee nodes.
- Each verifies the received proofs and computes .
- Committee nodes execute an MPC protocol to compute and each of them asserts that . adds to the .
- Credential issuance:
- Each committee node evaluates
and generates a partial signature .
- sends to .
- After decrypting partial signatures, obtains the full signature and constructs the master credential.
- Each committee node evaluates
- System Setup:
Context-based credential issuance
Master credentials are not used for making interactions with applications because of the resulting linkability and their limited claims. Therefore, users create context-based credentials.
- Each application specifies a unique context .
- For getting a credential for , a user submits the and a set of claims required by .
- The committee verifies the claims and issues a credential for in the same way as the master credential.
For this to work efficiently, two more challenges must be addressed: (i) it needs to be ensured that the new claims belong to the user holding the master credential else users can buy stolen accounts to add false claims; (ii) make pairwise DIDs, i.e., make credentials for different contexts independent.
- Claim validity: This is achieved by matching attributes in the new claim with the ones in the master credential. They have proposed the usage of linking attributes instead of using the attributes used for deduplication because the unique identifier (like SSNs) may not be used in all the services. In their implementation, they have used as the linking attribute. Users attach a ZKP to prove that the name used in the new claim is the same as that in the case of master credential. They have developed a fuzzy matching mechanism for matching names.
- Sybil-resistance within a context: A context-based credential should include the property to ensure that a user can issue only one credential per .
- Context-based credential issuance protocol: Each application specifies a .
- Let the user have a master credential .
- submits .
- The committee maintains a set of identifiers that have already received a credential.
- Finally, is added to the .
The usual issue of VCs is the applications colluding to figure out users’ usage patterns. The authors have mentioned that CanDID can be extended with suitable anonymous credentials for solving this purpose.
Credential verification
Any party using CanDID can verify user ’s context-based credential with associated and associated opened commitments. The verifying party makes three checks:
- is properly signed by the committee.
- does not appear in the public revocation list.
- Any commitment openings are valid.
Security arguments
- Sybil resistance: This follows from the integrity properties of oracle protocols.
- Unforgeability: Follows from the unforgeability of signatures.
- Privacy in credential issuance: From the privacy of oracle protocols, generating a pre-credential does not leak information about . In addition, since the commitment is hiding, and MPC evaluation of guarantees privacy, does not learn during issuance.
- Credential validity: Follows from the integrity of oracle protocols
- Unlinkability across applications: The only linkage between the master credential and context-based credentials lies in the . This property holds from the fact that an adversary cannot corrupt the committee members.
- Privacy in credential verification: Firstly, unopened commitments do not leak any information due to the hiding property. Secondly, commitments hide the result of a ZKP.
Accountability
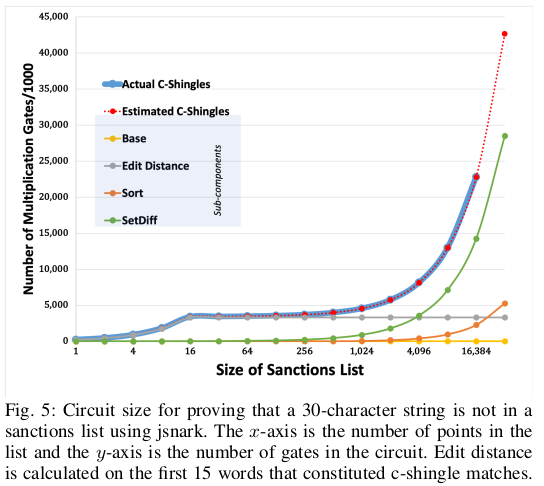
CanDID enforces accountability by identifying misbehaving individuals in a privacy-preserving manner. In their implementation, they have used sanction lists for this purpose. There are two related problems corresponding to this:
- Registration time compliance: When is created, the user has to show that their name is not in the sanctions list. The user produces a SNARK proof for solving this issue.
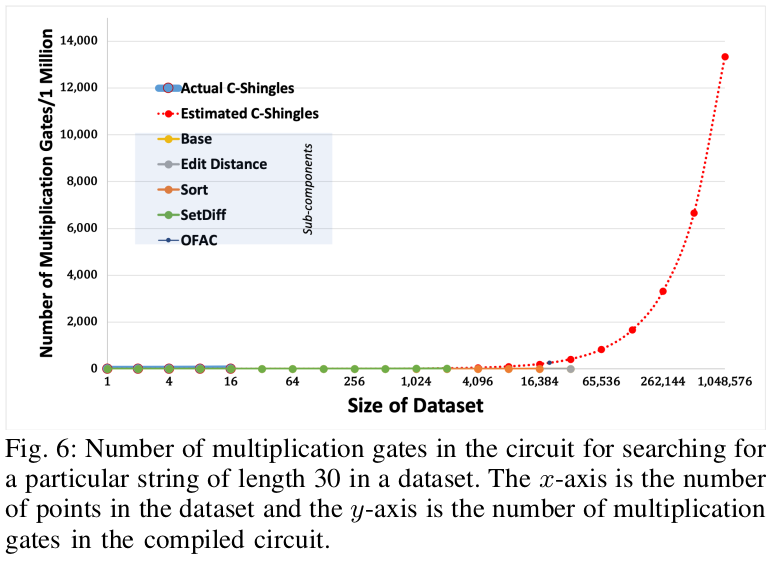
- Periodic Screening: If a new name is added to the revocation list, then CanDID must find out if a credential for the newly-added name exists in the sanction list. This implies that the whole and needs to be searched to find the names and their pseudonyms.
For both of them, the system must be able to detect potential alternate spellings of names. This is normally done by using fuzzy matching. The challenge in the case of CanDID is to do this in a secure manner.
For achieving this goal, they deployed a fuzzy matching algorithm based on edit distance and c-shingles. Evaluating edit distance requires a dynamic programming approach which has a large constant factor due to the size of the alphabet. Therefore, an approximation of edit distance has been used which is called c-shingles. The c-shingles of a word is the set of length consecutive substrings of (ignoring order, repetition). Let be the set of c-shingles of . We have from the c-shingles paper. If is the edit distance between , then the distance between and is given by:
c-shingles has been used as a filtering mechanism in this architecture. First, the intersection between c-shingles with every element is computed to obtain a set of matches, and then, the distance is computed on these. It should be noted that given and , the evaluation of edit distance is simply computing the intersection between two sets. Therefore, this process can be sped up by storing the c-shingles of every name in the dataset and the sanctions list. To do this securely, an oblivious sorting network is used to sort the dataset using the shingle distance, and then, the edit distance is computed only on a fixed number of candidates. For implementing this, the parameters chosen are as follows:
Max. length of name = 30
Edit distance threshold () = 3
c-shingles are used for removing the cases which cannot be matched. After setting the value of as 2, the number of candidates chosen for calculating the edit distance was 15 (). Next, the edit distance is calculated.
Computation using SNARK and MPC:
- For a client input string , compute the and provide a SNARK proof for the same.
- A boolean list is computed:
- Bitonic sort is used to sort using the condition . This pushes all the zero values to the back. The ones with the zero value are the ones that cannot have a distance less than .
- Retrieve the first elements from the . This gives the .
- Then, check if for .
In the end, a set is returned. If the set is empty, then nothing needs to be done. If that’s not the case, then: (i) the user may not be registered; (ii) the user may be expelled.
This procedure can be implemented as an arithmetic circuit which can then be compiled into either a R1CS for use with a SNARK (for the registration time screening) or as an MPC program (for periodic screening).
Key Recovery System
The standard DID and VC systems require users to store private key securely and reliably. This burdens the users. CanDID has a key-recovery subsystem that solves this issue. It deploys mechanisms similar to that in the identity system.
Users can store their DID keys with CanDID committee which stores users’ keys in a secret sharing manner. Users can employ legacy web authentication schemes to retrieve their backed-up keys. The users can choose their preferred authentication policies for recovery. The committee enforces the policy for key release.
This could have been done by using OAuth but this would bring up a major privacy issue - leakage of information to the CanDID committee members. Instead, CanDID uses privacy-preserving proof of account ownership, just like in the case of the identity system.
Enrollment: This is for backing up of key.
- picks a random ephemeral identifier and generates a pre-credential containing a commitment to ’s account identifier associated with the authentication provider (). The only difference here is that the contains a which prevents the correlation between the two systems.
- Pre-credentials are verified by using a verification protocol where the user proves knowledge of .
- The committee nodes run MPC to compute private key .
- The user then shares the secret shares of across the committee.
- stores .
Recovery:
To retrieve, the enrollment process is replicated to compute . fetches the and then, shares with the user.
Security Arguments:
- Unforgeability: This is followed because the committee nodes never get to know the backed-up private key.
- Key recovery privacy: Same as the credential privacy in the identity system.
Results
Pre-credential generation
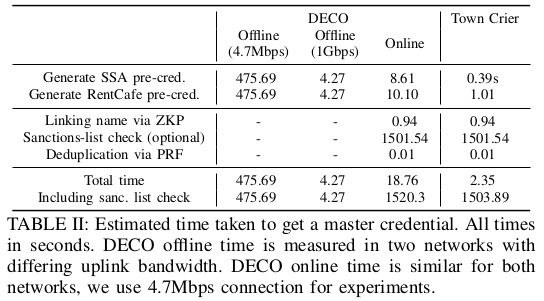
Master Credential Generation
- Proof of name matching across pre-credentials: Over 100 runs, the proof generation took 1.2 seconds, while verification took 0.006 seconds on average.
- Proof of non-existence in the sanctions list:
- Distributed PRF: 38 ± 1ms of CPU-time across four nodes in MP-SPDZ, as averaged over 10 trials of 10 runs each
Privacy-preserving screening via MPC
References