Introduction

This paper defines the notion of blind signatures with attributes that are based on Abe’s blind signature scheme [1] which is a modified version of the Schnorr scheme. In a blind signature with attributes, the signer and the user take a commitment $C$ to the user's attributes as input, and it outputs another (unlikable) commitment $\tilde{C}$ to the same attributes along with a signature on this commitment and a message of the user's choice. Note that taking the commitment to the user’s attributes as input gives the user the ability to prove in zero-knowledge that the committed data includes correct attributes.

Note that a blind signature with attributes can be used to construct an anonymous credential scheme as follows.

1. A user with some attributes can generate a commitment $C$ to his attributes.

2. He can prove in zero-knowledge that the commitment $C$ is generated from correct attributes.

3. He runs a blind signature with attributes with commitment $C$.

4. Now he can convince any verifier that he has a credential that includes the desired attributes as follows:
   1. He presents his signature and the output commitment $\tilde{C}$, and
   2. He proves in zero-knowledge that $\tilde{C}$ corresponds to those attributes.

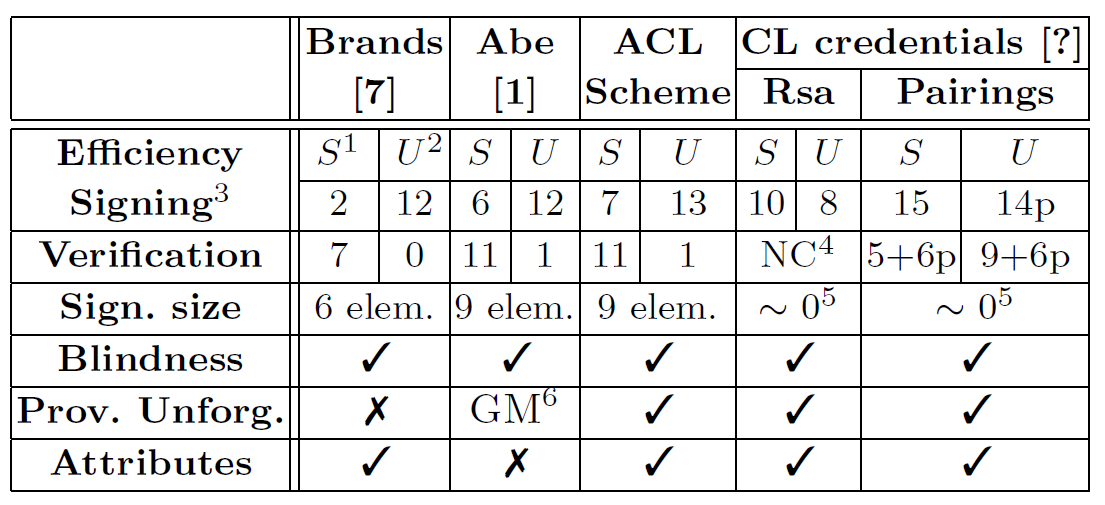
The importance of this paper is that it can work on the elliptic curve groups without pairings, which makes it more efficient. (see the below table)

Preliminary

OR-proof

An OR-proof is a $\Sigma$-protocol for a relation $R_L$ in which the prover and the verifier have the common inputs $h_0$ and $h_1$, and the prover knows an $x$ such that $(h_i,x) \in R_L$ for $i \in \{0,1\}$.

Generalized Pedersen commitment

The Pedersen commitment is based on discrete logarithm assumption. This paper uses a generalized version of the Pedersen commitment scheme on the set of messages $(L_1,\dots, L_n)$ as follows:

• Setup: Assume that the security parameter is $\kappa$, and the maximum number of messages is $n$. Let $G$ be a group with prime order $q=\Theta(2^{\kappa})$ with generators $h,h_1,\dots,h_n$. Let $R$ be randomness.

• Commit: $Commit(L_1,\dots,L_n;R) = h^R\prod_{i=1}^{n}h_i^{L_i}$, where $L_i \in \Z_q.$

Note that Pedersen commitment is information-theoretically hiding and computationally binding.

Combined commitment scheme

It is a combination of two commitments. For example, let us instantiate it with generalized Pedersen commitment. Assume that the generators are $h,h_0,\dots,h_n$. Assume we have two commitments as follows:

• $Commit_1(L_1,\dots,L_n;R_1) = h^{R_1} \prod_{i=1}^{n}h_i^{L_i}$

• $Commit_2(L_0;R_2) = h^{R_2} h_0^{L_0}$

Then the combined Pedersen commitment is $Commit(L_0, L_1, \dots, L_n; R = R_1 + R_2)$

Blinded Pedersen commitment scheme

The Pedersen commitment can be made blinded by an additional parameter $z\in G$, where $z \ne 1$. Assume that we have a commitment $C=Commit (L_1, \dots, L_n;R)$. Then the value $(z^{\gamma},C^{\gamma})$ can be seen as a blinded Pedersen commitment, i.e. $Commit^B (L_1, \dots, L_n;R,\gamma) = (z^{\gamma}, Commit (L_1, \dots, L_n;R)^{\gamma}).$

Assumption

The security of the proposed scheme is based on the Decisional Diffie-Hellman assumption and the Discrete-Logarithm assumption.

Notation and setup

• Let $G$ be a group of order $q$

• Let $g$ be a generator of $G$

• Let $H:\{0,1\}^*\to\Z_q$ be a hash function

• Assume a trusted party $TD$ chooses $params= (q,G,g,z,h,h_0,\dots,h_n)$ as system parameters, where $z,h,h_0,\dots,h_n \in G$ and $n$ is the maximum number of attributes that a user can have.

• The signer randomly selects a private key $x\in_R\Z_q$ and computes his real public key $y=g^x \pmod q$.

• Given $(G,q,g,h,y)$, the $TP$ outputs $z$ which is the tag public key of the signer.

• Therefore the public key of the signer is $(G,q,g,h,y,z)$, and the private key is $x$.

Anonymous Credential Light (ACL)

In a nutshell, the protocol proceeds as follows. The user and the signer take inputs as described in the below figure. The user commits ($C$) to certain attributes that he claims he has. Then the user proves in zero-knowledge that he knows an opening of the commitment $C$.

Then, the signer computes some one-time tag keys depending on randomness and the commitment $C$ and sends the randomness to the user so that he can check and compute the same one-time tag key.

The user computes another commitment $\tilde{C}$ which is a blinded Pedersen commitment to the same attributes. (See $\zeta, \zeta_1$ in the below figure)

The signer and the user perform two $\Sigma$ protocols ( using the OR-proof technique). In the end, the user forms the blind signature with attributes $\sigma$ that is an 8-tuple, i.e. $\sigma = (m, (\zeta, \zeta_1, \rho, \omega,\rho'= \{\rho_1',\rho_2'\}, \omega',\mu))$, where $\zeta_1$encodes the attributes of the user. Note that $\zeta, \zeta_1$ corresponds to the commitment $\tilde{C}$. (see the below figure)

Signature / Credential issuing

The signature issuing scheme is run in three phases, i.e. registration, preparation, and validation. The registration phase is a one-time phase that should be performed only once for each user. The preparation and validation phases may be performed simultaneously.

Single-Use Credentials

Single-use anonymous credentials avoid double use of the same credential. If a user uses anonymous credentials with the same attributes twice, the verifier can reveal the user’s identity.

First, the user computes another commitment $C_2 = Commit(L_0;R_2)$ for some random $(L_0;R_2)$ (recall the definition of the Combined commitment scheme). Note that $C_2$ is specific to the credential. Then user sends $C_2$ to the signer, and he also sends a zero-knowledge proof of the opening of $C_2$. The user and the signer participate in a blind signature protocol with the combined commitment $\tilde{C}$, i.e. commitment to the set of attributes $(L_0, L_1, \dots, L_n; \tilde{R})$.

To use this credential (with $\tilde{C}$)

• the user sends $(m, \tilde{C}, \sigma)$ to the verifier,

• the verifier sends a challenge $c$ to the user,

• the user reveals the equation ``double-spending equation” $cL_1 + L_0$ to the verifier,

• The user provides a zero-knowledge proof that this information was revealed correctly,

In case of double use of a credential, a verifier can simply compute $L_1$ (which is the user’s public key) from the double-spending equations.

Relevancy assessment

This paper proposes an anonymous credential scheme that depends on a blind signature with attributes. The underlying signature scheme is used for proving the knowledge of some secrets with some zero-knowledge techniques.

The solution uses a different security assumption from the known ones. This makes it suitable for lightweight devices compared to the solutions using bilinear pairings.

This solution may give us useful ideas about the construction of an anonymous credential with the property of double-use detection.

References

[1] Masayuki Abe. A secure three-move blind signature scheme for polynomially many signatures. In EUROCRYPT, pages 136{151, 2001. https://www.iacr.org/cryptodb/data/paper.php?pubkey=1981